分类讨论思想
学习方法 | 05-16 15:54 10916次 8次
麦肯锡有个分类法则,叫MECE法则。中文意思是“相互独立、完全穷尽”。简单来说,就是使用MECE法则分类,各个要素之间要保证不能有交叉,也不能有遗漏,也就是“不重不漏”。

举个例子,把人分为男人和女人,就符合MECE法则。因为从人的生理结构上来说,除了男人就是女人。
但如果把人分为男人和未婚女人,就有问题了,因为没有穷尽,把已婚女人给遗漏了;把人分为男人和已婚人士,又出现了重复,因为男人里边有已婚的,已婚里边有男人。
在信息分类的时候,MECE就好比一把尺子,可以用来判断信息要素是不是分类清楚了。
是不是觉得这个法则特别实用,其实它只是分类讨论数学思想在实际工作生活中的一种应用方式。
分类讨论思想
所谓分类讨论,就是在研究和解决数学问题时,当问题所给对象不能进行统一研究,我们就需要根据数学对象的本质属性的相同点和不同点,将对象区分为不同种类,然后逐类进行研究和解决,最后综合各类结果得到整个问题的解决,这一思想方法,我们称之为“分类讨论的思想”。
简而言之,就是把要研究的对象按照相同点和不同点分成各种不同情况分门别类加以讨论,然后把各种情况讨论出来的结果整合起来,是一种化繁为简的思维过程,考察学生的思维缜密性和全面性。

对问题实行分类与整合,确定分类标准后等于增加了一个已知条件,实现了有效增设,将大问题分解为小问题,优化解题思路,降低问题难度。
分类讨论的思想之所以重要,有四个原因:

一是它的逻辑性较强;二是它的知识点的涵盖比较广;三是它可培养学生的分析和解决问题的能力;四是实际问题中常常需要分类讨论各种可能性。
分类的原则
分类讨论也要遵循一定原则进行的,分类的对象是确定的,标准是统一的,每一部分是相互独立的,既不重复、也不遗漏。

原则1:按统一标准划分,比如,我们想知道班里的男生女生的平均身高,那么我们是不是要把班上所有学生分成男生,女生两类,而这个分类标准是性别。
原则2:不重不漏,就是被分后的各种情况不能有重叠部分而且合起来是整个研究对象的全部,如男生中不能有女生,同样,女生中不能有男生,而且男生加上女生要是全班的总人数。
原则3:按照等级先后顺序进行,有时候我们做一次分类还不够还需要对其中某些情况再分类。
常见的类型
类型1:由数学概念引起的的讨论,如实数、有理数、绝对值、点(直线、圆)与圆的位置关系等概念的分类讨论;
类型2:由数学运算引起的讨论,如不等式两边同乘一个正数还是负数的问题;
类型3 :由性质、定理、公式的限制条件引起的讨论,如一元二次方程求根公式的应用引起的讨论;
类型4:由图形位置的不确定性引起的讨论,如直角、锐角、钝角三角形中的相关问题引起的讨论。
类型5:由某些字母系数对方程的影响造成的分类讨论,如二次函数中字母系数对图象的影响,二次项系数对图象开口方向的影响,一次项系数对顶点坐标的影响,常数项对截距的影响等。
分类讨论思想是对数学对象进行分类寻求解答的一种思想方法,其作用在于克服思维的片面性,全面考虑问题。
中学考点分析
应用分类讨论的思想对问题求解,首先要明确讨论对象,确定对象的全体;其次是确定分类标准,分层次,不重复,不遗漏,达到互斥、无漏、最简的原则;
最后还要反思其过程,从中发现“分”与“合”,“局部”与“整体”之间的辨证统一关系,充分挖掘求解问题中潜在特殊性与简单性,尽可能地简化或避免分类讨论;使解题思想得到进一步升华,使解题的途径更加简洁的策略。
铛铛铛铛~又到了青果送福利时间了,下面,青果教育研究院院长常性军老师结合具体考点,针对“分类讨论思想”的具体运用,特别设计了以下经典题型,与你分享。
希望同学们可以认真理解,做一道题,学会一类题,一步行,千里亦能行。
分类讨论思想常见的六种类型
方程 若含有字母系数的方程有实数根时,要考虑二次项系数是否等于0,进行分类讨论。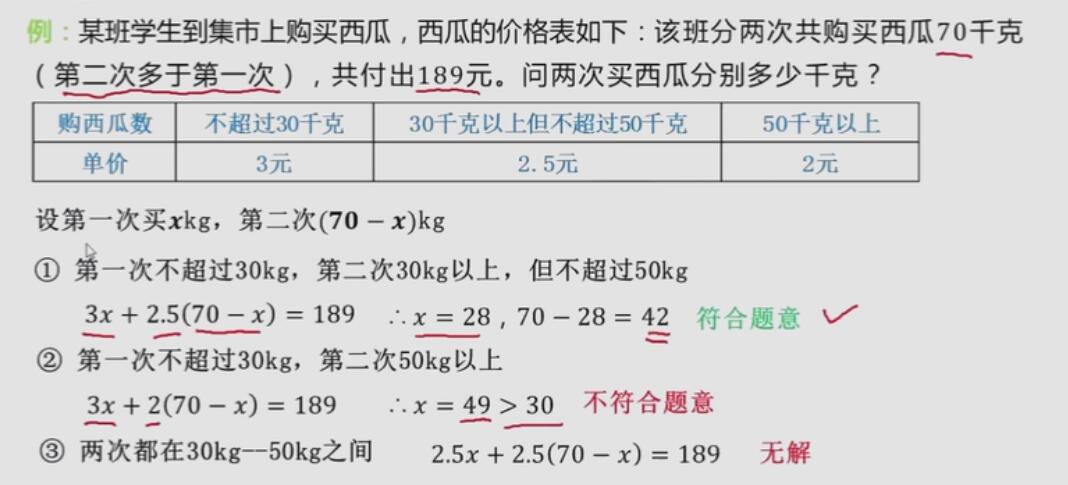
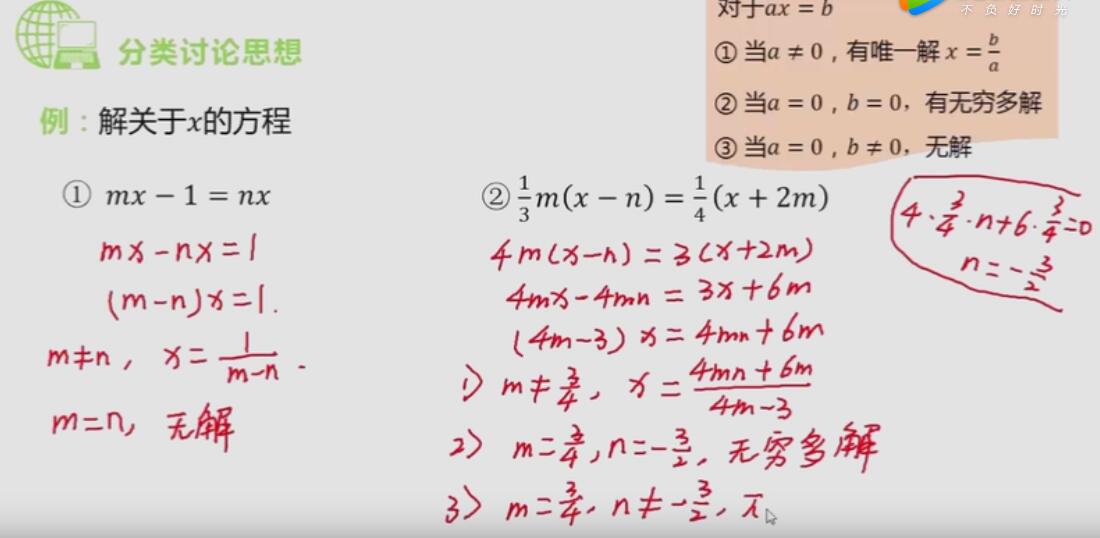
直角三角形 在直角三角形中给出两边的长度,确定第三边时,若没有指明直角边和斜边,要注意分情况进行讨论(分类讨论),然后利用勾股定理即可求解。

相似三角形 如果题目中出现两个三角形相似,需要讨论各边的对应关系;若出现位似,则考虑两个图形在位似中心的同旁或两旁两种情况讨论。 一次函数 已知一次函数与坐标轴围成的三角形的面积,求k的值,常分直线交于坐标轴正半轴和负半轴讨论;确定反比例函数与一次函数交点个数,常分一、三象限或二、四象限两种情况讨论。
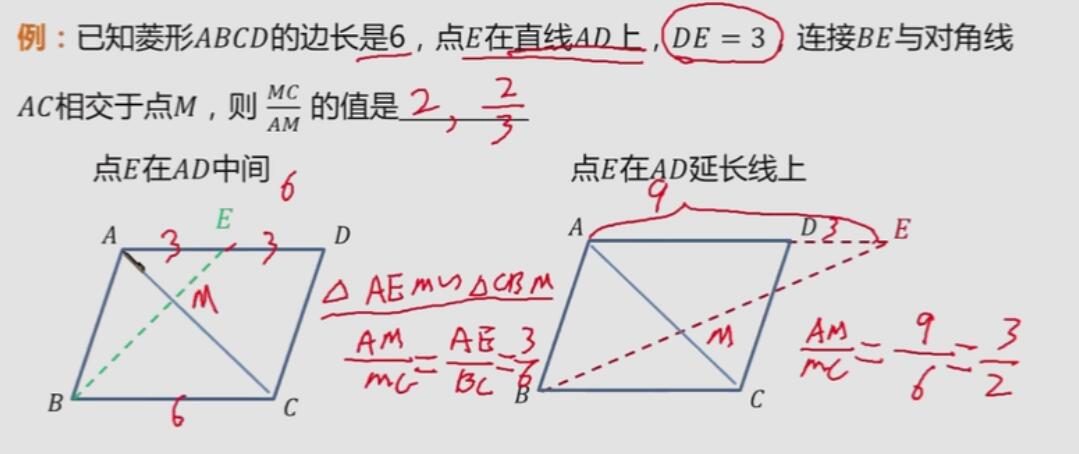



圆 圆的一条弦(直径除外)对两条弧,常分优弧和劣弧两种情况讨论;求圆中两条平行弦的距离,常分两弦在圆心的同旁和两旁两种情况讨论;圆与圆的相切,此时要考虑分外切和内切两种情况讨论。

当数学问题中的条件,结论不明确或题意中含参数或图形不确定时,就应分类讨论。
总而言之,应用分类讨论思想解决问题必须保证分类科学,标准统一,做到不重复,不遗漏,并力求最简。
化繁为简,破“简”成蝶!
8人赞